6.15 subgroups

Subgroups

R figure

Python figure

Code

import numpy as np
import matplotlib.pyplot as plt
from math import log2, sqrt

c = 1
pos = c * 50
neg = 50

def entropy(P, N):
    if P == 0 or N == 0:
        return 0
    p = P / (P + N)
    n = N / (P + N)
    return -p * log2(p) - n * log2(n)

def gini(P, N):
    p = P / (P + N)
    n = N / (P + N)
    return 4 * p * n

def dkm(P, N):
    p = P / (P + N)
    n = N / (P + N)
    return 2 * sqrt(p * n)

def minacc(P, N):
    p = P / (P + N)
    n = N / (P + N)
    return min(p, n)

def metric(tp, fp, m):
    if tp + fp == 0:
        return 0
    Pos = pos
    Neg = neg
    N = Pos + Neg
    TP = tp
    FP = fp
    FN = Pos - TP
    TN = Neg - FP
    if m == 'accuracy': return (TP + TN) / N
    if m == 'wracc': return TP / N - (TP + FP) * (TP + FN) / (N ** 2)
    if m == 'confirmation':
        A = (TP + FP) * (FP + TN) / (N ** 2)
        B = FP / N
        C = sqrt(A)
        return (A - B) / (C - A) if C != A else 0
    if m == 'generality': return (TP + FP) / N
    if m == 'precision': return TP / (TP + FP)
    if m == 'laplace-precision': return (TP + 10) / (TP + FP + 20)
    if m == 'f-measure': return 2 * TP / (2 * TP + FP + FN)
    if m == 'g-measure': return TP / (FP + Pos)
    if m == 'precision*recall': return TP ** 2 / ((TP + FP) * (TP + FN))
    if m == 'avg-precision-recall': return TP / (2 * (TP + FP)) + TP / (2 * (TP + FN))
    if m == 'aucsplit': return (TP * Neg + Pos * TN) / (2 * Pos * Neg)
    if m == 'balanced-aucsplit': return TP / Pos - FP / Neg
    if m == 'chi2': return ((TP * TN - FP * FN) ** 2) / ((TP + FP) * (TP + FN) * (FP + TN) * (FN + TN))
    if m == 'info-gain': return entropy(Pos, Neg) - (TP + FP) / N * entropy(TP, FP) - (FN + TN) / N * entropy(FN, TN)
    if m == 'gini': return gini(Pos, Neg) - (TP + FP) / N * gini(TP, FP) - (FN + TN) / N * gini(FN, TN)
    if m == 'dkm': return dkm(Pos, Neg) - (TP + FP) / N * dkm(TP, FP) - (FN + TN) / N * dkm(FN, TN)
    if m == 'entropy': return entropy(TP, FP) / 2
    if m == 'giniimp': return gini(TP, FP)
    if m == 'dkmimp': return dkm(TP, FP)
    if m == 'minacc': return minacc(TP, FP)
    return 0

def rocgrid():
    fig, ax = plt.subplots(figsize=(6, 6))
    ax.set_xlim(0, neg)
    ax.set_ylim(0, pos)
    ax.set_xticks(np.arange(0, neg + 1, 10))
    ax.set_yticks(np.arange(0, pos + 1, 10))
    ax.grid(True, color='gray', linestyle='--', linewidth=0.5)
    ax.set_xlabel('Negatives')
    ax.set_ylabel('Positives')
    return ax

def contour1(ax, m, color, linestyle, tp, fp):
    v = metric(tp, fp, m)
    if m == 'wracc':
        r = min(1 - 4 * v, 1)
        g = 2 * v + 0.5
        b = 0
    else:
        r = min(2 - 2 * v, 1)
        g = v
        b = 0
    plot_color = (r, g, b)
    lwd = 4 if linestyle == 'solid' else 2
    ax.plot(fp, tp, marker='o', color=plot_color, markersize=lwd)
    if tp == 0 or fp == 0:
        return
    x = np.arange(0, fp + 1)
    y = np.arange(0, tp + 1)
    Z = np.zeros((len(y), len(x)))
    for i, xi in enumerate(x):
        for j, yj in enumerate(y):
            Z[j, i] = metric(yj, xi, m)
    cs = ax.contour(x, y, Z, levels=[v], colors=[plot_color], linestyles=linestyle, linewidths=lwd - 1)

ax = rocgrid()
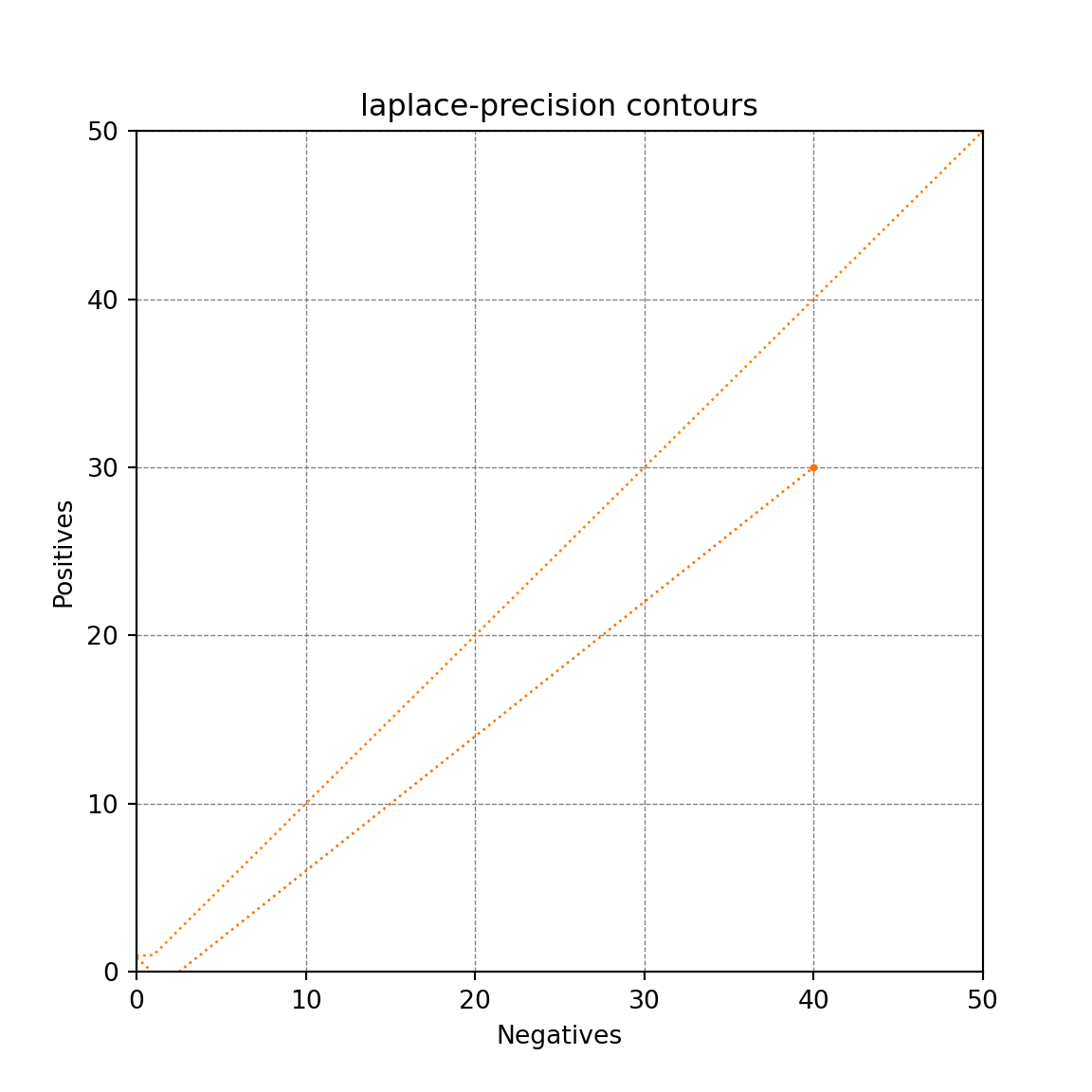
method = 'laplace-precision'
contour1(ax, method, 'black', 'dotted', 50, 50)
contour1(ax, method, 'black', 'dotted', 30, 40)
plt.title("laplace-precision contours")
plt.show()