2.5 Covroc left

In a coverage plot, accuracy isometrics have a slope of 1, and average recall isometrics are parallel to the ascending diagonal. In the corresponding ROC plot, average recall isometrics have a slope of 1; the accuracy isometric here has a slope of 3, corresponding to the ratio of negatives to positives in the data set.

R figure

Code

h <- 25 
w <- 75 
grid.step <- 5

TP1 <- 15
FP1 <- 15
TP2 <- 20
FP2 <- 20
TP3 <- 20
FP3 <- 30

plot( c(0,w), c(0,h),  
     xaxs = "i",yaxs = "i",
     xaxt = 'n', yaxt = 'n',
     type = "n",
     xlab = "Negatives", ylab = "Positives")

axis(2,c(0,TP1,TP2,h),labels=c('0','TP1','TP2-3','Pos'))
axis(1,c(0,FP1,FP2,FP3,w),labels=c('0','FP1','FP2','FP3','Neg'))

gx <- grid.step
while (gx <= w) {
  abline(v = gx, col="gray", lty="dotted")
  gx <- gx + grid.step
}
gy <- grid.step
while (gy <= h) {
  abline(h = gy, col="gray", lty="dotted")
  gy <- gy + grid.step
}

abline(c(0,h/w),col="gray")

abline(c(10,h/w),lty=2)
abline(c(0,1),lty=2)

col1 <- "blue"
points( FP1, TP1, col=col1, type="o")
text( FP1, TP1, "C1", pos=3)
abline(h=TP1, v=FP1, col=col1, lty="dotted")

col2 <- "red"
points( FP2, TP2, col=col2, type="o")
text( FP2, TP2, "C2", pos=3)
abline(h=TP2, v=FP2, col=col2, lty="dotted")

col3 <- "green"
points( FP3, TP3, col=col3, type="o")
text( FP3, TP3, "C3", pos=3)
abline(h=TP3, v=FP3, col=col3, lty="dotted")

Python figure

Code

import matplotlib.pyplot as plt
import numpy as np

h = 25
w = 75
grid_step = 5

TP1 = 15
FP1 = 15
TP2 = 20
FP2 = 20
TP3 = 20
FP3 = 30

fig, ax = plt.subplots()
ax.set_xlim(0, w)

(0.0, 75.0)

Code

ax.set_ylim(0, h)

(0.0, 25.0)

Code

ax.set_xticks([0, FP1, FP2, FP3, w])
ax.set_xticklabels(['0', 'FP1', 'FP2', 'FP3', 'Neg'])
ax.set_yticks([0, TP1, TP2, h])
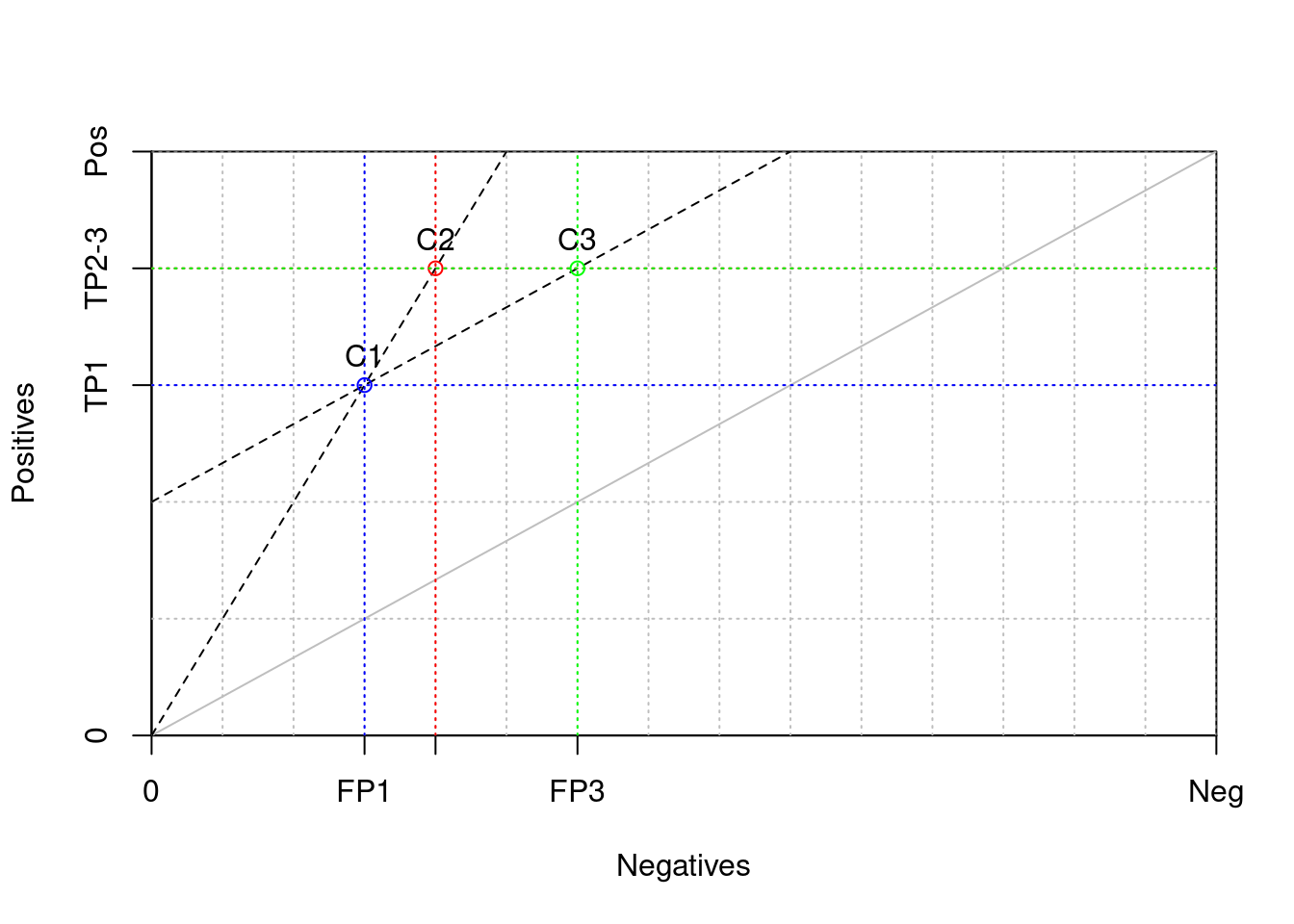
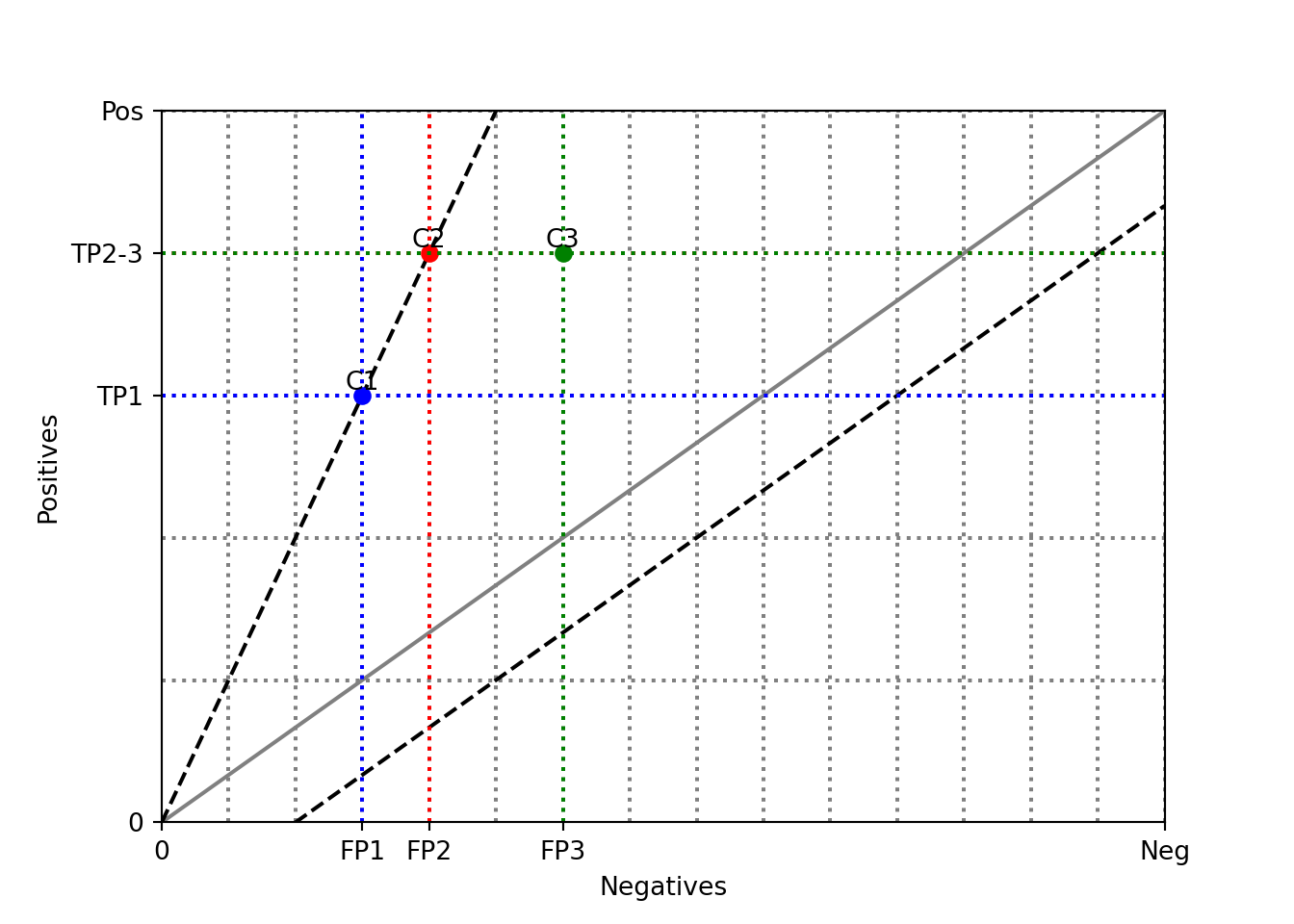
ax.set_yticklabels(['0', 'TP1', 'TP2-3', 'Pos'])

for gx in range(grid_step, w + 1, grid_step):
    ax.axvline(x=gx, linestyle='dotted', color='gray')
for gy in range(grid_step, h + 1, grid_step):
    ax.axhline(y=gy, linestyle='dotted', color='gray')

x_diag = np.array([0, w])
y_diag = (h / w) * x_diag
ax.plot(x_diag, y_diag, color='gray')

x_diag2 = np.array([0, w])
y_diag2 = x_diag2
ax.plot(x_diag2, y_diag2, linestyle='dashed', color='black')

x_diag3 = np.array([0, w])
y_diag3 = (h / w) * (x_diag3 - 10)
ax.plot(x_diag3, y_diag3, linestyle='dashed', color='black')

ax.plot(FP1, TP1, marker='o', color='blue')
ax.text(FP1, TP1, "C1", va='bottom', ha='center')
ax.axhline(y=TP1, color='blue', linestyle='dotted')
ax.axvline(x=FP1, color='blue', linestyle='dotted')

ax.plot(FP2, TP2, marker='o', color='red')
ax.text(FP2, TP2, "C2", va='bottom', ha='center')
ax.axhline(y=TP2, color='red', linestyle='dotted')
ax.axvline(x=FP2, color='red', linestyle='dotted')

ax.plot(FP3, TP3, marker='o', color='green')
ax.text(FP3, TP3, "C3", va='bottom', ha='center')
ax.axhline(y=TP3, color='green', linestyle='dotted')
ax.axvline(x=FP3, color='green', linestyle='dotted')

ax.set_xlabel("Negatives")
ax.set_ylabel("Positives")
plt.show()